Técnicas de Wave Field Synthesis (WFS) para arreglos de subs
WFS es una técnica de reproducción espacial de un campo sonoro con el objetivo de generar una percepción auditiva allí donde la imagen sonora se produce.
WFS es una técnica de reproducción espacial de un campo sonoro con el objetivo de crear una percepción auditiva allí donde la imagen sonora se produce.
La reproducción binaural consigue externalizar la percepción sonora con el uso de auriculares debido a su condición de aislamiento. A partir de la obtención, para diferentes grados, de la respuesta impulsional de cada individuo, podemos generar la sensación que el sonido se reproduce externamente alrededor de nuestra cabeza.
Con la misma idea se investigó la posibilidad de recrear el mismo efecto con altavoces dispuestos en una configuración 2.0.
La dificultad de esta técnica reside en que en la reproducción por altavoces ya no existe aislamiento entre los oídos y se produce un fenómeno denominado crosstalk. Parte de la señal emitida por el altavoz no únicamente llega al oído deseado, sino que también llega al oído contrario. Para solucionar este fenómeno debemos cancelar toda aquella parte de la señal que no queremos que llegue al oído no deseado. Esto se realiza con el uso de filtros inversos. Como los filtros de cancelación se eligen para una posición angular única, la reproducción binaural a través de altavoces también produce una posición de escucha óptima única.
A través de la reproducción de una línea de altavoces uniformemente distribuidos, WFS trata de generar una área de escucha óptima, es decir, un área donde percibir la fuente sonora allí donde se produce.
Un sistema de altavoces que rodea al oyente puede ser considerado como una condición límite de la ecuación de onda no homogénea. La solución de la ecuación de onda homogénea para una región acotada con respecto a las condiciones de contorno no homogéneas está dada por la integral de Kirchhoff-Helmholtz.
EL PRINCIPIO DE HUYGENS
Alrededor de 1860 el físico danés Huygens propuso un mecanismo simple para trazar la propagación de ondas. Su construcción es aplicable a ondas mecánicas en un medio material.
Si una onda es emitida por una fuente puntual con frecuencia (f), en cualquier instante de tiempo, todos los puntos del frente de ondas pueden ser considerados fuentes puntuales para la producción de una onda esférica de la misma frecuencia. Entonces, en el siguiente instante el frente de ondas es la envolvente de las ondas secundarias.
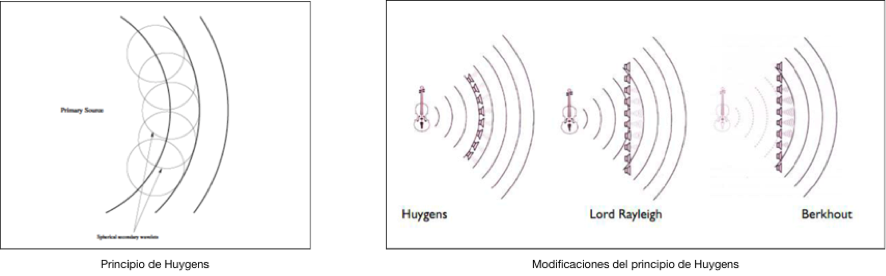
WFS es una aplicación directa del principio de Huygens. Con un array de altavoces el frente de ondas dentro de un volumen puede ser sintetizado. Cada altavoz del array actúa como una fuente secundaria para la creación de la onda y el sistema puede sintetizar un campo sonoro de una o varias fuentes virtuales situadas detrás de la línea de altavoces. Cada altavoz suena cuando el frente de ondas virtual pasa a través suyo.

a.- Principio básico de WFS | b.-Parámetros usados para la integral de Kirchoff-Helmholtz
La teoría de WFS asume una línea de altavoces infinita, cosa que evidentemente no puede ser asumida. Por lo tanto, una de las limitaciones para la creación del frente de ondas será debido a la longitud del array de altavoces. Esta limitación produce un fenómeno de difracción en los laterales debido al truncamiento de la línea. Truncar la longitud de la fuente secundaria puede ser entendido como un hueco en la propagación del campo sonoro.
Este efecto puede ser minimizado con el uso de algún tipo de ventana, suele ser habitual el uso de una “Square Cosine Window” a cambio de reducir el área efectiva de escucha.

Otro problema es la separación entre los elementos de la línea, las longitudes de onda de las frecuencias más agudas imposibilita su uso, ya que la máxima separación entre las fuentes vendrá determinada por la separación de los altavoces y el ángulo de incidencia respecto de la normal de la fuente virtual.

Donde “c” es la velocidad de propagación del sonido, “x” la separación entre altavoces y “Φ” el ángulo de incidencia de la fuente virtual.
Pero siempre y cuando esta condición se cumpla, podemos generar un campo sonoro y posicionar la imagen allí donde hayamos elegido.

Linea de altavoces

Como podemos observar en el gráfico, si no se cumple la ecuación del alias espacial el sistema colapsa y no es capaz de construir el campo sonoro.
Y que tiene que ver la teoría de WFS en el desarrollo y diseño de un arreglo de subs? Pues que podemos utilizar esta teoría para modificar su directividad, construir arcos o minimizar sus lóbulos secundarios.
Veamos un ejemplo: Queremos crear una línea de 8 altavoces separados 2 metros y simular una fuente virtual que llega con 45º respecto de la normal.
Para ello necesitaremos obtener el delay relativo de cada fuente y su relación de intensidad. Los cálculos de distancia y por lo tanto los cálculos de delay pueden ser realizados de varias maneras, pero posiblemente el más cómodo sea usar la distancia euclidea en base a las coordenadas cartesianas de la posición de la fuente virtual y los altavoces.
Aunque WFS puede simular un campo 3D, por razones obvias, una línea de subgraves estará posicionado con todos los altavoces a la misma altura, por lo tanto, podemos eliminar de los cálculos la coordenada Z.
Calculamos en primer lugar la frecuencia a la que se producirá el alias espacial:
 El siguiente paso es calcular los delays de cada altavoz:
El siguiente paso es calcular los delays de cada altavoz:
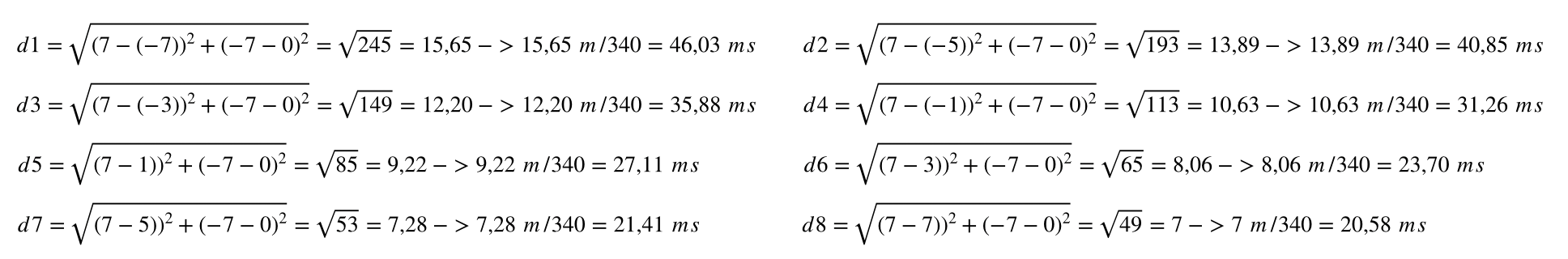
Estos tiempos de delay posicionarían la fuente virtual allí donde se ha diseñado. Este puede ser un buen recurso para la generación de efectos pero en el caso de querer crear direccionalidad en una línea de subgraves no tiene sentido aplicar tanto delay, por lo tanto, tomaremos no la diferencia absoluta sino la relativa entre altavoces, así los tiempos de delay definitivos sería la diferencia entre cada altavoz y el altavoz de menor tiempo:
![]()
Una vez calculados los tiempos de delay simplemente necesitamos conocer la atenuación de cada altavoz. Tomamos como valor de máxima intensidad el altavoz de menor delay y como valor de referencia 1, de este modo podemos calcular la atenuación relativa como:

Una vez obtenidas las atenuaciones de cada altavoz en relación a la distancia normalizamos para encontrar el tiempo relativo. Las atenuaciones son:

Veamos la respuesta del arreglo a diferentes frecuencias:

APLICACIÓN PRÁCTICA
Es evidente que no tiene demasiado sentido forzar el arreglo a ángulos exagerados respecto la normal ni atenuar el volumen de los altavoces. Pero esta idea puede ser útil en determinados casos. Veamos varios ejemplos:
LÍNEA DE SUBS VOLADA
En una configuración de PA y sub volado los ejes del cada array apuntan a lugares distintos.

Directividad baja frecuencia para el array de altavoces

Directividad línea de subgraves
En el caso que quisiéramos enviar la energía de la línea de subgraves al mismo lugar que el sistema de PA, deberíamos angular la linea de subs

Linea de subs angulada mecánicamente
Usando el concepto anteriormente explicado, podemos simular el comportamiento de la línea de subs angulada mecánicamente con el uso de delays

Angulación de la linea de subs aplicando delays
CONSTRUIR UN ARCO ELECTRÓNICO DE SUBS
Esta misma técnica nos puede servir para desarrollar un arco electrónico. En este caso simularemos la fuente virtual en el eje de la línea de altavoces, es decir, con un ángulo de 90º respecto de la normal.
Recordemos que la longitud de una arco queda determinada por el radio y el ángulo.
Si queremos desarrollar un arco con 8 subgraves separados 2m y un ángulo de 40º deberemos conocer el valor del radio.

Arco de 8 subs en ángulo de 40º
La ecuación de la longitud de un arco:

El aliasing espacial se producirá para: 
Una vez obtenido el radio podemos encontrar los valores de delay:

El arco es simétrico, por lo que solamente es necesario obtener los valores para la mitad de altavoces. Obviamos la atenuación por distancia en este ejemplo
Respuesta del arreglo a diferentes frecuencias:



En el siguiente gráfico podemos observar la respuesta de magnitud y fase:

Verde: Respuesta a 0º | Azul: Respuesta a 20º
REDUCIR LÓBULOS LATERALES
Cómo se explica anteriormente, un truncamiento en una línea de altavoces puede ser vista como un hueco en la propagación de la onda. En la técnica de WFS se aplican correcciones enventando las esquinas laterales del arreglo para minimizar los lóbulos laterales.
En una configuración de subs podemos simular el enventanado disminuyendo el nivel de los altavoces laterales
Este sería el resultado:



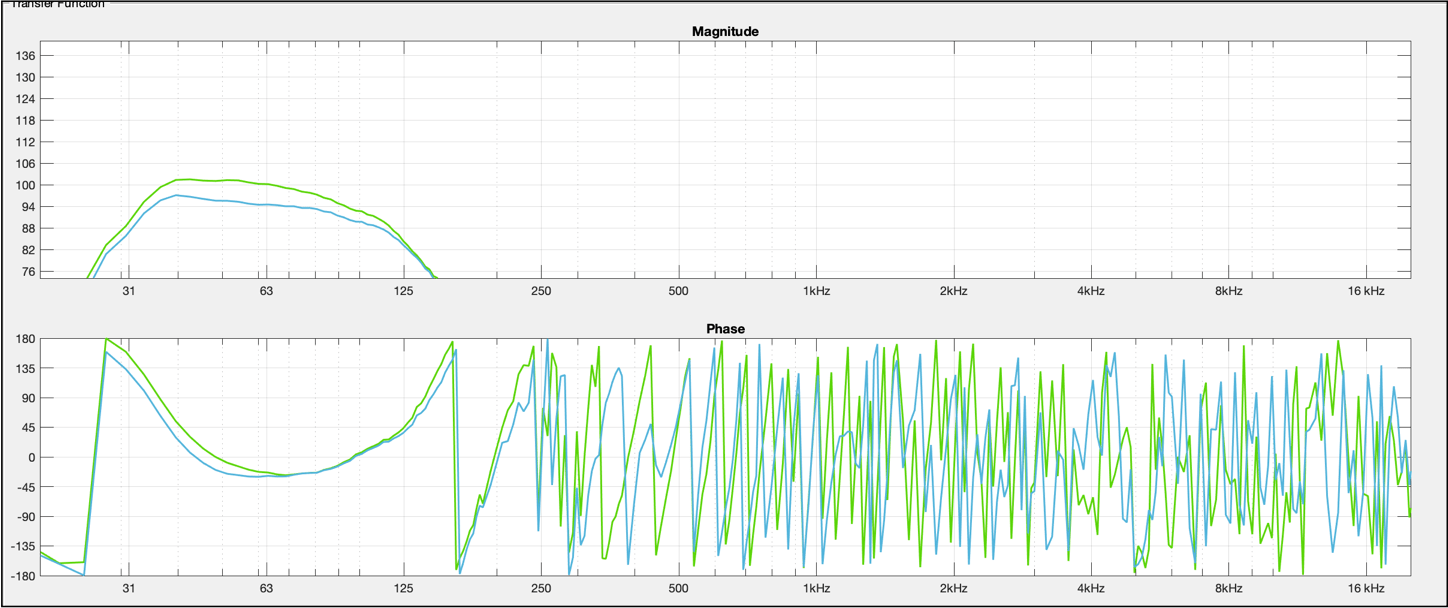
Verde: Respuesta a 0º | Azul: Respuesta a 20º





ariston andrade silva
14 noviembre, 2019 at 2:04 pmquero agradecer pelo o belo post, sensacional !
Juan Antonio Padilla Garcia
25 noviembre, 2019 at 8:15 pmMe quito el sombrero Pepe. Genial
Sony a Torres
14 enero, 2020 at 5:44 pmBuenas tardes 🙂 me ha encantado el post, no suelo comentar en blogs pero aqui estoy! Un abrazo y gracias por el blog, sin duda un post muy pero que muy completo
kili
26 abril, 2020 at 8:29 pmHola Pepe,
Muchas gracias por el post, muy interesante.
¿Podrías compartir la bibliografía de donde has extraído la teoria?
Gracias anticipadas,
Un saludo.
prova_prova
27 abril, 2020 at 9:37 amHola,
Esta técnica la estudié hace años en Audio 3D. Creo recordar que obtuve información aquí: Montag Thesis 2011 – Wave Field Synthesis in Three Dimensions by Multiple Line Arrays
Aunque este Post basado en WFS es una idea própia
Saludos
Kili
27 abril, 2020 at 12:30 pmGracias nuevamente