2- Optimización de Sistemas, Suma de señales
Vimos en el artículo anterior, conceptos generales, un método sencillo que nos permite expresar cualquier diferencia de tiempo o distancia en grados, a partir de la frecuencia y la velocidad angular. Seguiremos profundizando sobre este concepto.
La suma de señales es lineal y, como veremos, depende de la relación de fase. Estudiemos este concepto
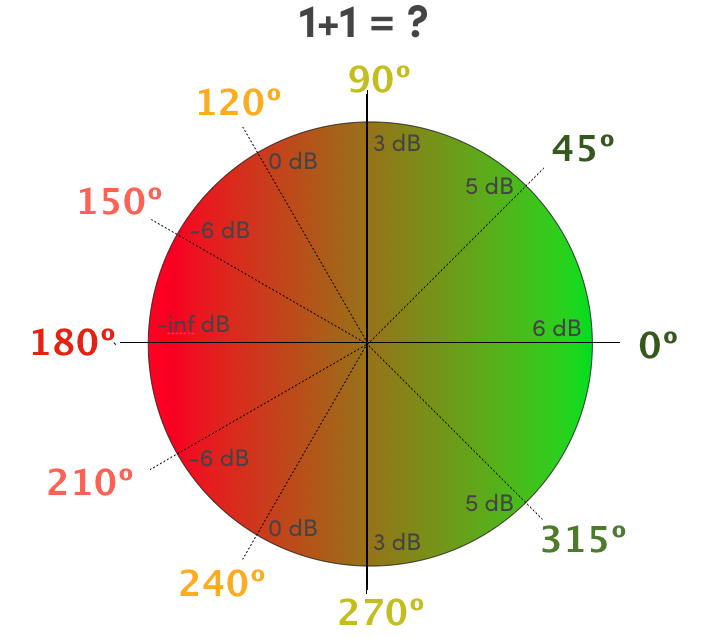
El siguiente gráfico nos hace una pregunta: Cuánto es 1 + 1 ?
Ahora bien, sí tratamos con señales correlacionadas, como la mayoría de señales que manipulamos en ajuste de sistemas, 1 + 1 puede ser cualquier valor entre -∞ y 2. Y este resultado depende de la relación de fase y del nivel relativo.
La rueda de fase nos ayuda a conocer cuál será el resultado de suma dependiendo de esta diferencia de tiempo o distancia. El gráfico asume que las señales son correlacionadas y exactamente con el mismo nivel.
Recordemos, podemos utilizar el círculo como una representación gráfica del periodo o de la longitud de onda, por lo tanto, para relacionar el tiempo o la distancia en grados necesitaremos conocer la frecuencia
Si nos fijamos con detalle en el gráfico, podemos apreciar como cambia de color desde un color verde (suma máxima) a un color rojizo (cancelación máxima)
Para comprobar que el resultado de la rueda de fase se cumple utilizaremos la suma de señales de manera compleja para visualizar la forma de onda combinada (tiempo) y una analizador FFT para visualizar su espectro (frecuencia)
El siguiente gráfico muestra una sinusoide de frecuencia 1 kHz y su respuesta espectral
 Sinusoide 1 kHz / Respuesta espectral
Sinusoide 1 kHz / Respuesta espectral
En los siguientes ejemplos comprobaremos que sucede al desplazar una señal respecto de otra determinado tiempo y compararemos su resultado respecto a la respuesta espectral y de nivel de una única sinusoide. (1.2)
Diferencia relativa 0º (1 + 1 = 2), 6 dB
Cuando 2 señales se encuentran con una diferencia relativa de 0º su relación de suma es máxima, en este caso 1 + 1 = 2. Que expresado en logarítmico es igual a aproximadamente 6 dB. Ambas señales están en el mismo tiempo.
 Suma de 2 señales con diferencia relativa de 0º / Respuesta espectral
Suma de 2 señales con diferencia relativa de 0º / Respuesta espectral
Diferencia relativa 90º (1 + 1 = √2 ), 3 dB
Calculemos en primer lugar a cuanto tiempo equivale 90º para 1 kHz. Si cambiamos circulo por ciclo fácilmente podremos hablar en grados
1 circulo de 1 kHz mide 1 ms, por lo tanto 90º equivale a una cuarta parte de tiempo: 1 ms / 4 = 0.25 ms
En este caso, como podemos ver en el gráfico de la rueda de fase su relación de suma será +3dB
 Suma de 2 señales con diferencia relativa de 90º / Respuesta espectral
Suma de 2 señales con diferencia relativa de 90º / Respuesta espectral
Diferencia relativa 120º (1 + 1 = 1 ), 0 dB
120 grados para 1 kHz equivale a un tercio del circulo, o lo que es lo mismo 0,33 ms.
En este caso 2 señales suman lo mismo que una única señal. Llegado a este punto siempre me gusta hacer esta broma “ Si quieres que 2 subgraves te suenen a uno, llévate uno”. Evidentemente es una exageración, porque en este ejemplo solamente estamos analizando una única frecuencia.
 Suma de 2 señales con una diferencia relativa de 120º / Respuesta espectral
Suma de 2 señales con una diferencia relativa de 120º / Respuesta espectral
Diferencia relativa 150º (1 + 1 = 0.5 ), -6 dB
150 grados para 1 kHz equivale a 0.416 ms. La suma de 2 señales da como resultado el valor de medio.
 Suma de 2 señales con una diferencia relativa de 150º / Respuesta espectral
Suma de 2 señales con una diferencia relativa de 150º / Respuesta espectral
Diferencia relativa 180º (1 + 1 = 0), -∞ dB
180 grados para 1 kHz equivale a 0.5 ms. Podríamos definir esta diferencia como el punto crítico, ese lugar donde se produce la mayor atenuación. matemáticamente -∞
 Suma de 2 señales con una diferencia de 180º / Respuesta espectral
Suma de 2 señales con una diferencia de 180º / Respuesta espectral
Aunque pueda parecer lo mismo, estas dos señales no tienen polaridad distinta, tienen una diferencia de tiempo de 180º. Un cambio de polaridad no implica un cambio de tiempo o distancia, simplemente significa cambiar el signo de la señal.
Recordemos que solemos expresar el sonido como un movimiento, un movimiento de ida y vuelta a su posición de equilibrio. Por lo tanto, es suficiente conocer que sucede durante un ciclo para saber que va a suceder. Realmente solo es necesario conocer que sucede en medio ciclo (medio circulo) ya que una vez superados los 180º el proceso se vuelve a repetir de manera inversa, como se puede apreciar en la simetría de valores de la rueda de fase.
Para terminar veamos 2 ejemplos más. Entender bien este breve apartado nos aportará mucha información para cuando estemos realizando funciones de transferencia, reduciendo el ancho de banda de los datos que tendremos que analizar
Qué diferencia de fase tienen los siguientes gráficos ?
 a) Diferencia de 360º b) Diferencia de 180º + polaridad
a) Diferencia de 360º b) Diferencia de 180º + polaridad
Caso a: Las señales están separadas exactamente un ciclo. Académicamente podríamos decir que estás dos señales tienen la misma fase. Pero si visualizamos el gráfico, claramente observamos que no tenemos el mismo tiempo.
Por lo tanto, diremos que estas dos señales vibran en el mismo estado pero no tienen el mismo tiempo.
Como iremos viendo, cada vez que dos frecuencias se encuentran a una diferencia de un múltiplo entero de 360º (0º,360º,…,n x 360º) ambas vibran en el mismo estado y por lo tanto obtienen la máxima suma.
Caso b: Las señales están separadas 180º pero tienen una diferencia de polaridad. Cuando dos frecuencias se encuentran con una diferencia relativa de un múltiplo entero impar de 180º (180º, 540º, …., (2*n+1) x 180º) ambas vibran en el mismo estado y obtienen la máxima suma.
Como conclusión de este razonamiento demostraremos que cuando dos pendientes de fase cruzan y la coherencia es buena significa que ambas frecuencias vibran en el mismo estado. Es decir, o bien un múltiplo entero de 360 grados o un múltiplo entero impar de 180 grados.






Rigoberto Antonio Cerrato Flores
12 diciembre, 2022 at 6:16 pmI want to learn more about using the software
Global Audio Solutions
12 diciembre, 2022 at 7:47 pmWe will also make videos on how to use RiTA
Daniel
13 diciembre, 2022 at 10:12 pmIncreíblemente ilustrativo el último gráfico.
Altaph mohammed
1 enero, 2023 at 11:28 amPlease make available in English
Global Audio Solutions
11 abril, 2023 at 6:36 pmSoon we will make a collection of videos on how to use RiTA to analyse without noise.